Cyfry rzymskie, Liczby rzymskie

Cyfry rzymskie – zapożyczone ze starożytnego Rzymu, to nie tylko system notacji liczbowej, ale także bogate dziedzictwo kulturowe, które przetrwało próbę czasu. 👴
To unikalne symbole, od prostego 'I' aż do skomplikowanego 'MMMCMXCIX'.

Zapraszam do materiału 👇

Cyfry rzymskie – wprowadzenie

Z tego materiału dowiesz się:

• Jakie były początki liczb rzymskich?
• Jaka jest struktura i zasady zapisu liczb rzymskich?
• Jak wygląda reprezentacja cyfr rzymskich w kodzie?
• Jakie są praktyczne zastosowania cyfr rzymskich?
• Jak zaimplementować przykładowy algorytm operujący na cyfrach rzymskich?

Historia cyfr rzymskich

Historia cyfr rzymskich (bez zaskoczenia...) rozpoczyna się w starożytnym Rzymie, gdzie pierwsze próby zapisu liczb miały formę liter alfabetu łacińskiego, od jedności „I” do tysiąca „M”.

Z biegiem czasu te literowe symbole ewoluowały w bardziej złożone znaki, takie jak „V” czy „X”, zyskując praktyczne zastosowanie w życiu codziennym starożytnych Rzymian.

Liczby rzymskie nie tylko zdobiły budowle i miały znaczenie w kalendarzach, ale także stanowiły integralną część architektury, finansów i kultury tamtej epoki. Dzięki tej fascynującej historii liczby rzymskie przetrwały wieki, pozostawiając ślad nie tylko w księgach matematyki, ale również w zakamarkach starożytnego życia. To nie tylko zapis cyfr, lecz tajemnica przeszłości, która wciąż kształtuje naszą dzisiejszą matematyczną świadomość.

Cyfry rzymskie – struktura i zasady zapisu

Cyfry rzymskie opierają się na kilku podstawowych znakach:

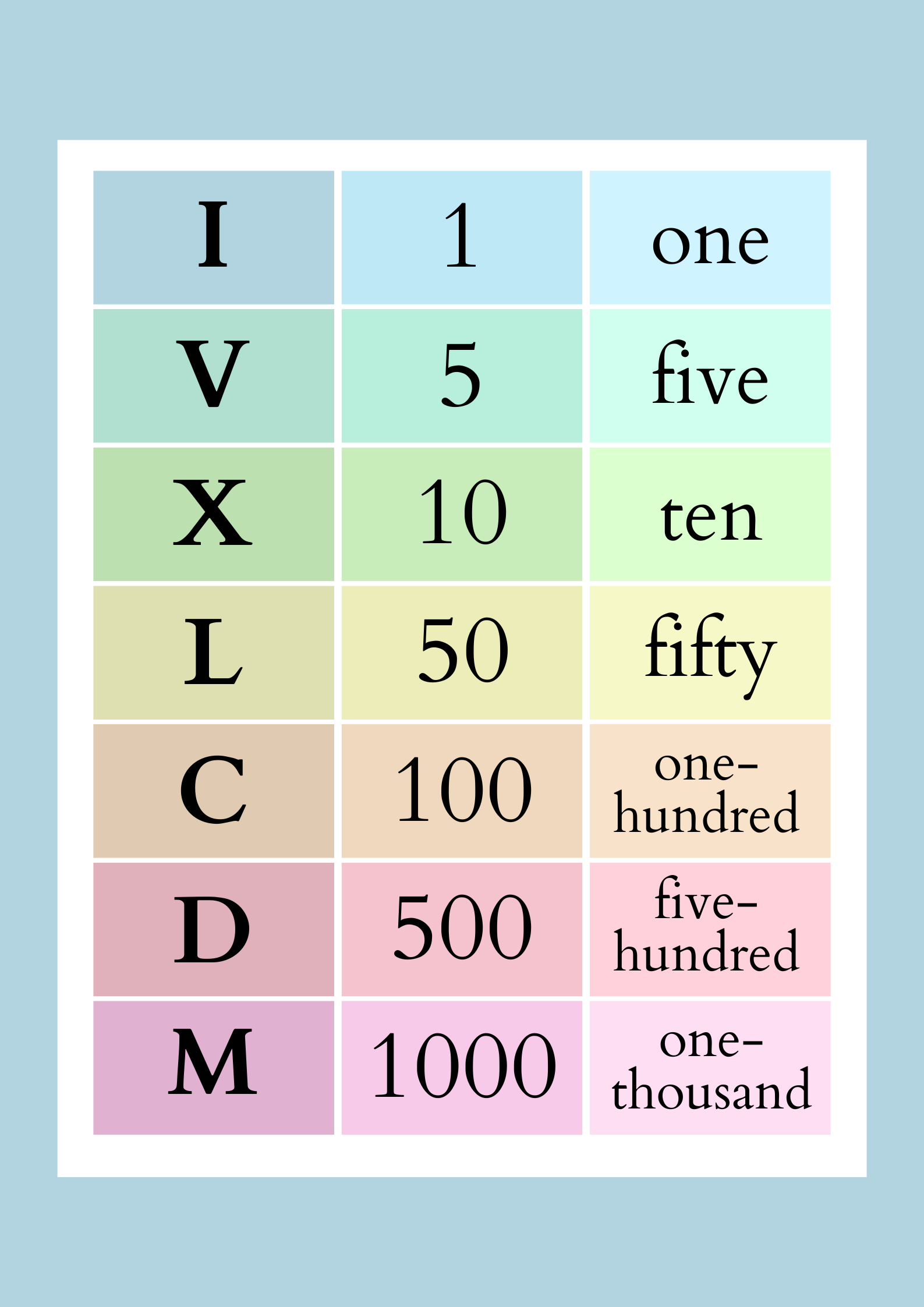
Znaki te są używane do konstruowania większych liczb poprzez ich kombinacje i zastosowanie poniższych reguł.

Podstawową zasadą jest sumowanie wartości liter. Jednak istnieje pewna finezja, np. IX oznacza 9, bo jest to 10 (X) minus 1 (I).
Takie podejścia zapewnia elastyczność i oszczędność znaków.

Pozostałe przykłady:

• II to 1 + 1 = 2
• VI to 5 + 1 = 6
• IXX to 20 – 1 = 19
• XXV to 10 + 10 + 5 = 25

Cyfry rzymskie – reprezentacja w kodzie

Pierwszym krokiem jest zrozumienie, jak reprezentować cyfry rzymskie w języku programowania.
Przyjrzymy się różnym podejściom i omówimy, które z nich są bardziej czytelne i efektywne.

Tablica mapowania

Jednym z najczęstszych podejść jest wykorzystanie tablicy do mapowania cyfr rzymskich na odpowiadające im wartości numeryczne.
To proste rozwiązanie ułatwiające konwersję obiektów w kodzie.

    Map romanToDecimal = new HashMap<>();
    romanToDecimal.put('I', 1);
    romanToDecimal.put('V', 5);
    romanToDecimal.put('X', 10);
    romanToDecimal.put('L', 50);
    romanToDecimal.put('C', 100);
    romanToDecimal.put('D', 500);
    romanToDecimal.put('M', 100);

→ ZOBACZ 👉: Struktury danych » Algorytmy i Struktury Danych

Enum do reprezentacji cyfr

Możemy również wykorzystać typ enum, aby zdefiniować cyfry rzymskie.
To może sprawić, że nasz kod będzie bardziej czytelny i modularny.

public enum RomanNumeral {
    I(1), V(5), X(10), L(50), C(100), D(500), M(1000);

    private final int value;

    RomanNumeral(int value) {
        this.value = value;
    }

    public int getValue() {
        return value;
    }
}

→ ZOBACZ 👉: Java enum

Cyfry rzymskie – praktyczne zastosowania

W dzisiejszym świecie programowania znacznie częściej wykorzystuje się cyfry arabskie. Mogą zdarzyć się jednak zadania gdzie trzeba będzie obsłużyć cyfry rzymskie. Najczęstszym przypadkiem będzie obsługa dat albo danych wprowadzanych przez użytkownika z użyciem cyfr rzymskich. Może się to przydać również w przypadku pisania różnego rodzaju konwerterów.

→ ZOBACZ 👉: System dwójkowy 0⃣1⃣ Binarna reprezentacja liczb | System Binarny 🆚 Dwójkowy

Cyfry rzymskie – algorytmy

Konwersja dziesiętna do systemu rzymskiego

class DecimalToRomanConverter {

        private static final TreeMap decimalToRomanMap = new TreeMap<>();

        static {
            decimalToRomanMap.put(1, "I");
            decimalToRomanMap.put(4, "IV");
            decimalToRomanMap.put(5, "V");
            decimalToRomanMap.put(9, "IX");
            decimalToRomanMap.put(10, "X");
            decimalToRomanMap.put(40, "XL");
            decimalToRomanMap.put(50, "L");
            decimalToRomanMap.put(90, "XC");
            decimalToRomanMap.put(100, "C");
            decimalToRomanMap.put(400, "CD");
            decimalToRomanMap.put(500, "D");
            decimalToRomanMap.put(900, "CM");
            decimalToRomanMap.put(1000, "M");
        }

        public String convertToRoman(int decimalNumber) {
            StringBuilder romanNumber = new StringBuilder();
            int floorValue = decimalToRomanMap.floorKey(decimalNumber);

            if (decimalNumber == floorValue) {
                romanNumber.append(decimalToRomanMap.get(decimalNumber));
                return romanNumber.toString();
            }

            while (decimalNumber > 0) {
                int closestFloorValue = decimalToRomanMap.floorKey(decimalNumber);
                romanNumber.append(decimalToRomanMap.get(closestFloorValue));
                decimalNumber -= closestFloorValue;
            }

            return romanNumber.toString();
        }

• Tworzymy TreeMap, który przechowuje pary klucz-wartość dla wartości dziesiętnych i odpowiadających im symboli rzymskich.
• Przechodzimy przez wartości w odwróconej kolejności, zaczynając od największych. Dla każdej wartości sprawdzamy ile razy może być ona pomniejszona od danej liczby dziesiętnej i dodajemy odpowiednią ilość symboli rzymskich do wyniku.
• Proces powtarzamy, aż osiągniemy wartość 0.

Warto zauważyć, że należało dodać do TreeMap więcej par niż potrzebujemy. Jak na przykład "IV" lub "IX". Dodanie tych specjalnych przypadków do mapy jest konieczne, aby algorytm poprawnie obsługiwał te wyjątkowe sytuacje i generował poprawne zapisy liczb rzymskich. Gdybyśmy tego nie zrobili, algorytm mógłby próbować skorzystać z kombinacji standardowych cyfr, co doprowadziłoby do błędnego zapisu liczby. Na przykład, dla liczby 4 algorytm użyłby "IIII" zamiast poprawnego "IV".

Konwersja z systemu rzymskiego na dziesiętny

class RomanToDecimalConverter {

    private static final Map romanToDecimalMap = new HashMap<>();

    static {
        romanToDecimalMap.put('I', 1);
        romanToDecimalMap.put('V', 5);
        romanToDecimalMap.put('X', 10);
        romanToDecimalMap.put('L', 50);
        romanToDecimalMap.put('C', 100);
        romanToDecimalMap.put('D', 500);
        romanToDecimalMap.put('M', 1000);
    }

    public int convertToDecimal(String romanNumber) {
        int result = 0;
        int prevValue = 0;

        for (int i = romanNumber.length() - 1; i >= 0; i--) {
            int currValue = romanToDecimalMap.get(romanNumber.charAt(i));

            if (currValue < prevValue) {
                result -= currValue;
            } else {
                result += currValue;
            }

            prevValue = currValue;
        }

        return result;
    }

W tej implementacji algorytm przechodzi przez cyfry rzymskie od ostatniej do pierwszej. Jeśli wartość aktualnej cyfry jest mniejsza niż wartość poprzedniej, odejmujemy ją od wyniku. W przeciwnym razie dodajemy ją do wyniku.
Dzięki takiemu podejściu mamy poprawną konwersję z systemu rzymskiego na dziesiętny.

Cyfry rzymskie – podsumowanie