Najdłuższy Wspólny Prefiks i Najdłuższy Wspólny Podciąg

Najdłuższy wspólny prefiks i najdłuższy wspólny podciąg to dwa istotne pojęcia w dziedzinie algorytmów i przetwarzania ciągów znaków.

Najdłuższy wspólny prefiks i najdłuższy wspólny podciąg – wprowadzenie

Z tego materiału dowiesz się:

• Czym jest najdłuższy wspólny prefix?
• Co to jest drzewo typu Trie?
• Jak zaimplementować algorytm znajdujący najdłuższy wspólny prefix?
• Czym jest najdłuższy wspólny podciąg?

Najdłuższy wspólny prefiks

Najdłuższy wspólny prefiks to najdłuższy początkowy fragment dwóch lub więcej ciągów znaków.
Na przykład, dla ciągów „program” i „projekt”, najdłuższy wspólny prefiks to „pro”.

Najdłuższy wspólny prefiks jest używany np. aby zidentyfikować wspólną część początkową w ciągach, co jest przydatne w zadaniach, takich jak porównywanie ciągów znaków, analiza słów kluczowych itp.

Podczas wyliczania najdłuższego wspólnego prefiksu możemy wykorzystać drzewo Trie (nie mylić z tree!).

Drzewo Trie

Drzewo Trie (zwane również drzewem prefixowym lub cyfrowym) jest strukturą danych specjalnie zaprojektowaną do przechowywania i przeszukiwania zestawów ciągów znaków.

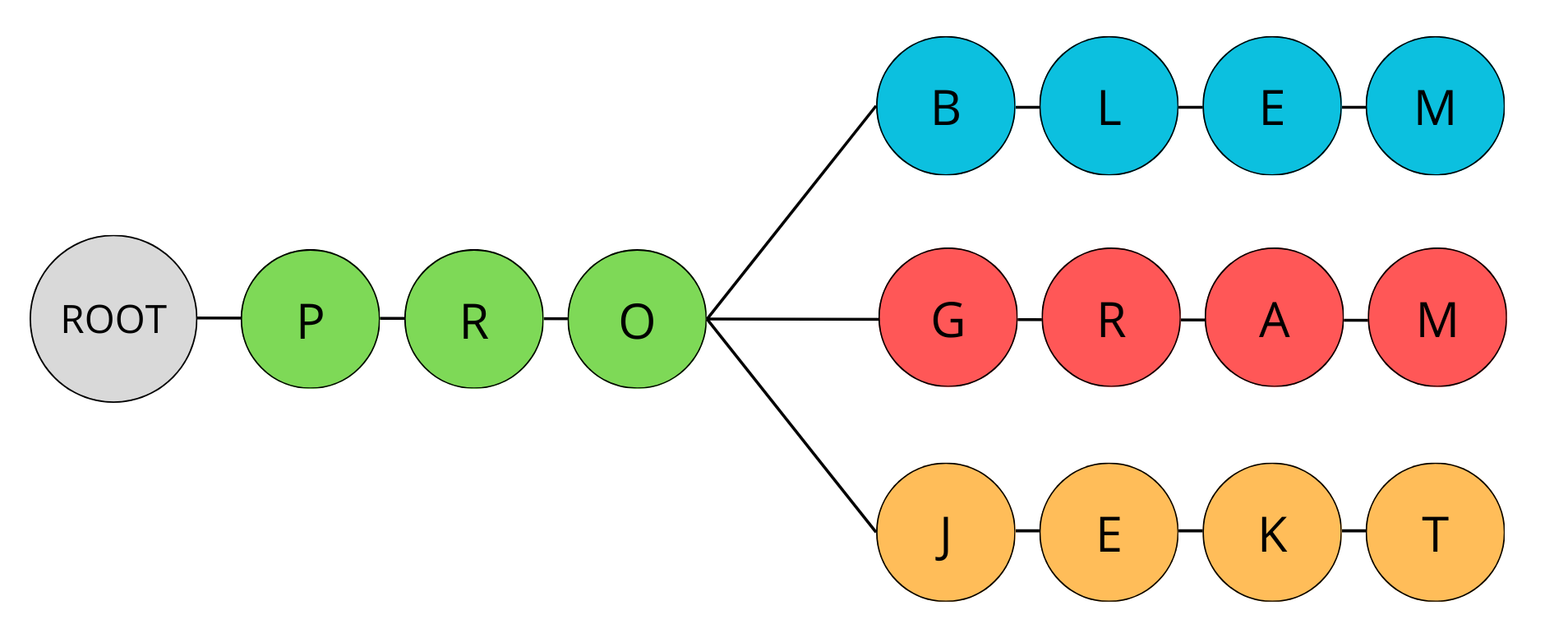
Zaletą drzewa Trie jest to, że pozwala na wydajne znajdowanie wspólnego prefiksu ciągów znaków, ponieważ przechowuje je w formie drzewa, gdzie wspólny prefiks dla wielu ciągów jest wspólną ścieżką w drzewie.

Algorytmy oparte na drzewach Trie często mają lepszą wydajność niż podejścia oparte na porównywaniu znak po znaku.

class TrieNode {
    Map<Character, TrieNode> children = new HashMap<>();
    boolean isEndOfWord = false;
}

class TrieNodeMain {
    public static String findLongestCommonPrefix(String[] strs) {
        if (strs == null || strs.length == 0) {
            return "";
        }

        TrieNode root = new TrieNode();

        for (String str : strs) {
            TrieNode node = root;
            for (char c : str.toCharArray()) {
                node.children.putIfAbsent(c, new TrieNode());
                node = node.children.get(c);
            }
            node.isEndOfWord = true;
        }

        StringBuilder prefix = new StringBuilder();
        TrieNode node = root;

        while (node.children.size() == 1 && !node.isEndOfWord) {
            Map.Entry<Character, TrieNode> entry = node.children.entrySet().iterator().next();
            prefix.append(entry.getKey());
            node = entry.getValue();
        }

        return prefix.toString();
    }
}

Powyższa metoda przyjmuje jako argument tablicę String. Po sprawdzeniu, czy tablica jest pusta inicjuje węzeł drzewa Trie. W kolejnym etapie iteruje po dostarczonych ciągach znaków, a następnie po znakach w bieżącym ciągu. Dalej w pętli dodawany jest nowy węzeł dla każdego znaku jeśli taki jeszcze nie istnieje. Tworzy obiekt StringBuilder do przechowywania wynikowego prefiksu. Na koniec w pętli while szuka najdłuższego prefixu.

➡ ZOBACZ 👉: StringBuilder: czy zawsze taki szybki? | String vs StringBuilder vs StringBuffer

Algorytm znajdujący najdłuższy wspólny prefix

Do znalezienia najdłuższego wspólnego prefixu możemy wykorzystać alternatywne rozwiązania. O to jedno z nich.

    public static String findLongestCommonPrefix(String[] strs) {
        if (strs == null || strs.length == 0) {
            return "";
        }

        String prefix = strs[0];

        for (int i = 1; i < strs.length; i++) {
            while (strs[i].indexOf(prefix) != 0) {
                prefix = prefix.substring(0, prefix.length() - 1);
                if (prefix.isEmpty()) {
                    return "";
                }
            }
        }
        return prefix;
    }

Tutaj podobnie jak w poprzedniej implementacji na start dostarczamy tablicę z ciągami znaków.
Rozpoczynamy od pierwszego ciągu, a następnie stopniowo skracamy go, porównując z pozostałymi ciągami, aż znajdziemy wspólny początek.
Ewentualnie zwrócimy pusty ciąg, jeśli nie ma wspólnego fragmentu.

➡ ZOBACZ 👉: String – najważniejszy typ danych

Najdłuższy wspólny podciąg

Najdłuższy wspólny podciąg (ang. Longest Common Subsequence, LCS) to najdłuższy ciąg znaków, który występuje w tej samej kolejności w obu łańcuchach. Znaki te mogą być rozdzielone w każdym z łańcuchów innymi znakami.

[LCS] to nie tylko teoretyczny problem algorytmiczny. Rozumienie tego zagadnienia ma praktyczne zastosowania.
Pozwala między innymi na porównywanie tekstów, znajdowanie wspólnych sekwencji w danych genetycznych czy śledzenie zmian w dokumentach.

    public static String lcs(String s1, String s2) {
        int m = s1.length();
        int n = s2.length();

        int[][] dp = new int[m + 1][n + 1];

        for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= n; j++) {
                if (i == 0 || j == 0) {
                    dp[i][j] = 0;
                } else if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }

        int lcsLength = dp[m][n];
        char[] lcs = new char[lcsLength];
        int i = m, j = n;
        while (i > 0 && j > 0) {
            if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
                lcs[lcsLength - 1] = s1.charAt(i - 1);
                lcsLength--;
                i--;
                j--;
            } else if (dp[i - 1][j] > dp[i][j - 1]) {
                i--;
            } else {
                j--;
            }
        }

        return new String(lcs);
    }

Powyższy fragment kodu źródłowego oblicza najdłuższy wspólny podciąg między dwoma ciągami znaków text1 i text2 przy użyciu programowania dynamicznego. Algorytm przechodzi przez oba ciągi znaków, tworząc tablicę dp do przechowywania wyników pośrednich. Następnie odtwarza najdłuższy wspólny podciąg, korzystając z tablicy dp.

➡ ZOBACZ 👉: String – konwertowanie i zamiana typów: Array, ArrayList, Char, Int, Integer

Najdłuższy wspólny prefiks | Najdłuższy wspólny podciąg – podsumowanie

Powyższe algorytmy mogą być użyteczne w rozwiązywaniu problemów, takich jak porównywanie dokumentów tekstowych, analiza sekwencji DNA, zarządzanie wersjami oprogramowania i wiele innych. Dodatkowo [LCS] może być stosowany w różnych dziedzinach, w których istnieje potrzeba znajdowania wspólnych sekwencji między dwoma ciągami znaków. Algorytm ten jest efektywny i ma wiele praktycznych zastosowań.